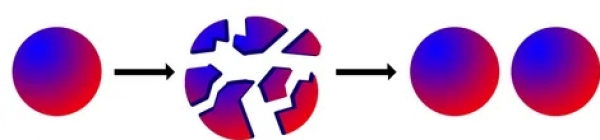
Представьте себе, что у вас был шар. Вы разбили его, а потом из осколков собрали два точно таких же новых шара. При этом осколки вы никак не обрабатывали - не подтачивали и не подрезали. Только комбинировали и перемещали. Ну и так получилось, что линии разрыва фрагментов должны были бы срастись идеально. Налицо нарушение закона сохранения материи!
Что же, вам наверняка кажется, что физически это невозможно? Очень похоже на фантастику? И правильно кажется! С физической точки зрения реализовать это не получится. Зато это можно сделать математически.
Мы только что познакомились со знаменитым парадоксом Банаха-Тарского.
Парадокс Банаха-Тарского - это тезис из математики, который утверждает, что можно разложить твердый шар на конечное число элементов, а затем собрать эти части, используя только вращения и перемещения, чтобы сформировать два твердых шара того же размера, что и исходный. Или можно сделать наоборот. Этот парадокс опирается на неизмеримую теорию множеств и не нарушает никаких физических законов.
Однако парадокс Банаха-Тарского не может быть реализован в физическом мире. Это связано с тем, что парадокс предполагает существование неизмеримых множеств, которые являются теоретическими математическими конструкциями, не имеющими физического аналога. В реальном мире любой физический объект, в том числе и твердый шар, может быть измерен последовательным и осмысленным образом, а его объем всегда четко определен.
Кроме того, парадокс Банаха-Тарского требует способности делить и собирать объекты на бесконечно малые части, что физически невозможно из-за ограничений, налагаемых законами физики, такими как дискретная природа материи на атомном и субатомном уровнях.
Ну а для того, чтобы любая математическая теорема могла быть применима в реальном мире, мы полагаемся на то, что математическая модель является достоверным и точным описанием реальности. По сути, мы полагаемся на правильность нашей научной теории.
Парадокс Банаха-Тарского опирается на свойства прямой вещественного числа, которые не моделируют реальность. В частности, возможность создания неизмеримых подмножеств, о которых уже было отмечено выше. В действительности каждый кусочек любого твердого тела имеет вполне определенный положительный объем, поэтому научная теория, опирающаяся на это свойство действительных чисел, несостоятельна. Теорема Банаха-Тарского не может быть доказана, если мы ограничимся измеримыми подмножествами. Проблема в том, что цель любой математической модели состоит в том, чтобы сделать рассуждения более простыми (или даже возможными), чем они есть в реальной жизни, и континуальные свойства вещественных чисел, которые позволяют проводить исчисление, были потрясающе эффективны в этом. В принципе, любая научная теория может допустить ненадлежащее использование вещественных чисел. Это подчёркивает тот факт, что нечто, будучи математической теоремой, не делает его автоматически «истинным» в реальном мире. И знаете что, тут вспоминаются "хейтеры" математической физики.
✅ Поддержать проект монеткой или задать вопрос можно тут! Здесь же я публикую фрагменты будущей книги, которую могут читать подписчики